Optimizing Neural Networks with Reinforcement Learning A Survey of Current Techniques

Abstract

Machine learning (ML) has transformed different sectors by allowing for data-based decision-making and forecasting analysis. This survey explores the integration of reinforcement learning with deep neural networks, highlighting applications in robotics, natural language processing, and games. It examines how RL optimizes complex policies, leveraging neural networks for function approximation. Challenges such as scalability, sample efficiency, and stability in training are discussed. Recently, the machine learning research trend expands to the system performance optimization field, where it has still been proposed by researchers based on their intuitions and heuristics. Compared to conventional major machine learning research areas such as image or speech recognition, machine learning-based system performance optimization fields are at the beginning stage.

Introduction

I. INTRODUCTION

Artificial intelligence (AI) includes machine learning (ML), which has emerged as a game-changing technology with the potential to revolutionise a number of industries, Reinforcement Learning  (RL) has gained prominence as a method for learning sequential decision-making tasks, with deep learning enhancing its ability to generalize across high-dimensional spaces. The paper introduces key RL algorithms, including Q-learning and policy gradients, and their role in optimizing neural network training dynamics. The introduction underscores the importance of using RL to address computationally hard optimization problems. Neural networks play a critical role in encoding complex problem states, offering flexibility and scalability compared to traditional optimization methods. The synergy between RL and neural networks for dynamic learning is a key focus. . AI is a vast field that aims to create intelligent machines [1]. Machine learning (ML) is a branch of AI that recognizes and learns different data set patterns [2].

Finding the optimal TSP solution is NP-hard, even in the two-dimensional Euclidean case [3], where the nodes are 2D points and edge weights are Euclidean distances between pairs of points. In practice, TSP solvers rely on handcrafted heuristics that guide their search procedures to find competitive tours efficiently. Even though these heuristics work well on TSP, once the problem statement changes slightly, they need to be revised. In contrast, machine learning methods have the potential to be applicable across many optimization tasks by automatically discovering their own heuristics based on the training data, thus requiring less handengineering than solvers that are optimized for one task only.[4]. Table 1 classifies different machine learning algorithms according to their learning types and specific categories. The table includes four main types of learning: Supervised Learning, Unsupervised Learning, Semi-Supervised Learning and Reinforcement Learning. This table provides a systematic understanding of various algorithms in the field of machine learning and presents from an academic perspective.

Table 1: Different types of ML algorithm

While most successful machine learning techniques fall into the family of supervised learning, where a mapping from training inputs to outputs is learned, supervised learning is not applicable to most combinatorial optimization problems because one does not have access to optimal labels. However, one can compare the quality of a set of solutions using a verifier, and provide some reward feedbacks to a learning algorithm. Hence, we follow the reinforcement learning (RL) paradigm to tackle combinatorial optimization. We empirically demonstrate that, even when using optimal solutions as labeled data to optimize a supervised mapping, the generalization is rather poor compared to an RL agent that explores different tours and observes their corresponding rewards.

II. ARTIFICIAL NEURAL NETWORKS

An ANN is a cluster of multiple perceptrons or neurons at each layer; when the input data is sorted in the forward direction, this is called the feed-forward neural network [15,77]. The basic structure of an ANN consists of three layers: the input layer, hidden layers, and output layer. The input layer receives the input data; the hidden layers compute the input data, and the output layer provides outcomes. Each layer’s duty in the neural networks attempts to learn specific decimal weights to be set at the end of the learning process. The ANN approach is good for solving image data, text data, and tabular data problems. The advantage of ANN is its skill of dealing with nonlinear functions and learning weights that help map any input to the output for any data. The architecture of the artificial neural network is shown in Figure 1. Each neuron output includes an activation function of a sum of all inputs weights.

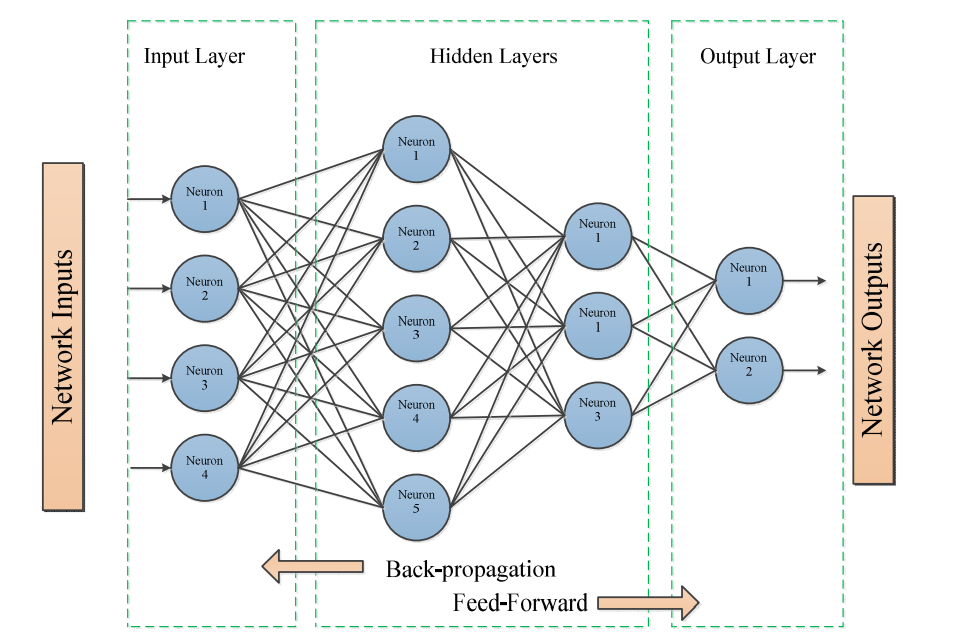
Figure 1: Artificial neural network architectures

III. REINFORCEMENT LEARNING ALGORITHMS

In the introduction section 1 we gave the definitions of an MDP, which include the states, actions, rewards, and transition functions. We also explained what the policy of an agent is and what is the optimal policy. Here we will deep-dive into the RL algorithms that search for the optimal policy of an MDP. Broadly, the RL algorithms can be split into the model-based and model-free categories  Figure 2.

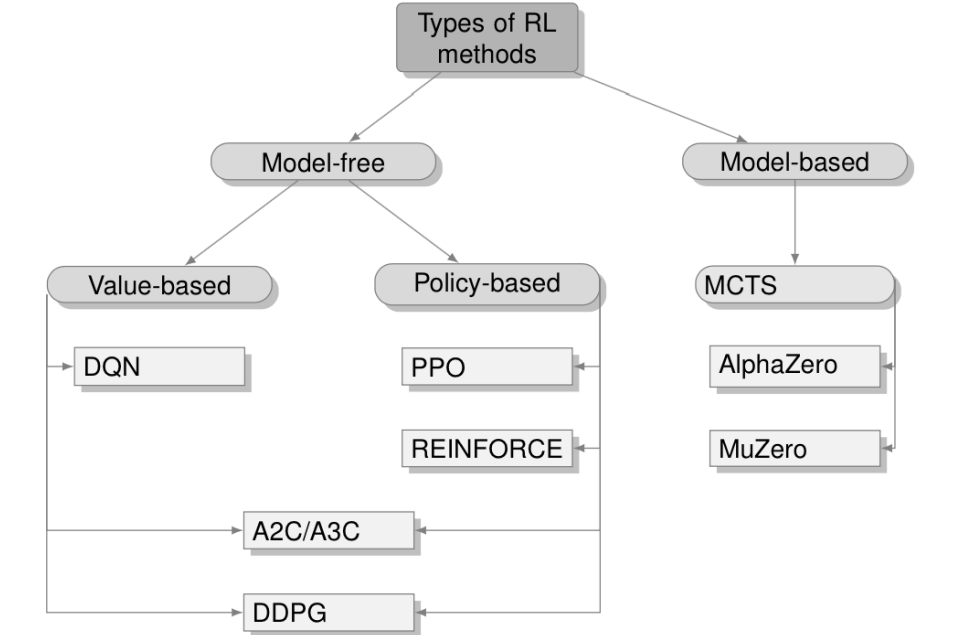
Figure 2: A classification of reinforcement learning methods.

1. Model-based methods focus on the environments, where transition functions are known or can be learned, and can be utilized by the algorithm when making decisions. This group includes Monte-Carlo Tree Search (MCTS) algorithms such as AlphaZero [9,8]
2. Model-free methods do not rely on the availability of the transition functions of the environment and utilize solely the experience collected by the agent.

IV. RELATED WORK

A. Neural Architecture Search (NAS)

A significant portion of research focuses on using reinforcement learning (RL) for neural architecture search, which automates the design of network architectures. RL agents are trained to select optimal neural configurations based on performance metrics[11].

B. Hyperparameter Optimization

Reinforcement learning has been extensively employed to tune hyperparameters dynamically during neural network training. Studies highlight how actor-critic or Q-learning models adjust learning rates, batch sizes, and dropout rates in real time, improving model generalization and convergence speed. [12]

??????????????C. RL-Assisted Weight Pruning

To make neural networks more efficient, RL is utilized in weight pruning, where unnecessary connections are removed. RL agents learn pruning strategies to balance model size and accuracy. [13].

???????D. Integration of Evolutionary Algorithms (EAs) and RL

Recent works explore the synergy between RL and EAs to optimize neural networks. [14]

V. MODEL COMPRESSION AND KNOWLEDGE DISTILLATION

RL also assists in compressing large neural networks and optimizing their deployment on edge devices. [15]

These areas demonstrate how RL has become a cornerstone in optimizing neural networks for efficiency, scalability, and application-specific performance.

The application of neural networks to combinatorial optimization has a distinguished history, where the majority of research focuses on the Traveling Salesman Problem (Smith, 1999). One of the earliest proposals is the use of Hopfield networks (Hopfield & Tank, 1985) for the TSP. The authors modify the network’s energy function to make it equivalent to TSP objective and use Lagrange multipliers to penalize the violations of the problem’s constraints. A limitation of this approach is that it is sensitive to hyperparameters and parameter initialization as analyzed by (Wilson & Pawley, 1988). Multi-layer Perceptron,  It is a regression-based neural network to improve sorting performance. The overall framework consists of three stages: the input phase is a step of pre-processing the input data, the sorting phase is a step of sorting the data by repeatedly inputting data into the model. Finally, there is a polish phase to correct inaccurately sorted elements to produce an accurate result.[16].

1. Perceptron: It is a perceptron-based reuse predictor to improve the accuracy of reuse prediction. However, an actual neural network is not applied, it only brought an idea of a perceptron. The multiple inputs are given, and it is indexed each weight table using input and PC, and it conducts prediction by adding each weight.[17].
2. LSTM: It replaces a hash-function with LSTM to increase the space utilization rate of inverted indexing. The architecture consists of a total of four stages: Input Stage is pre-processing data, Disperse Stage distributes the sub-models uniformly, Mapping Stage maps the sub-data to a local hash, and the Join Stage creates a global hash table.[18].

VI. MACHINE LEARNING BASED INDEX STRUCTURES

Traditional data management systems use a heuristic-based algorithm, which means that they do not utilize the characteristics of specific applications and data themselves [16].

In order to improve these problems, the papers [19] introduce a new index structure that leverages machine learning. In paper [20], three well-known index structures (B-Tree, Hash-Map, Bloom filter) are re-designed with machine learning-based techniques. Ref. [8] also proposes an inverted index based on machine learning.

??????????????A. Learned Hash-Map

A Hash-Map uses hash-functions to map the position in the array. The goal of the learned Hash-Map is to reduce the hash conflict [18]. To address the problem, they replace the hash-function with a machine learning-based model. They used a regression-based model. The model is also modeled as CDF for the key distribution, and it also uses RMI like the range index, in figure 3, when the trained model receives a key as an input, it predicts the position of the key in the array, similar to a hash function.

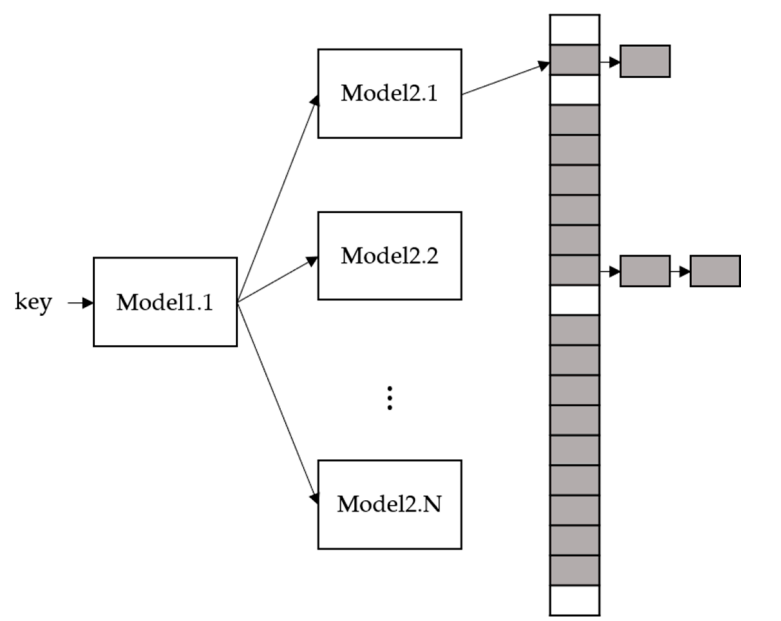
Figure 3: Learned Hash-M

???????B. Learned B-Tree

B-Tree index model predicts a position of look-up key within a sorted set of keys. Original B-Tree guarantees that found the key is the first key or higher than the look-up key. In addition, B-Tree determines whether the look-up key is in the page through binary search. In Figure 4, the upper-level model receives the key as input and predicts the next-level model until it is located at the lowest level. Upon reaching the lowest level model, the model predicts the location of the queried key and finds the queried key between min_err and max_err of the predicted location. In this paper [21], a regression-based range index is proposed. For the Learned B-Tree design, the Recursive Model Index (RMI) [22] was designed to increase accuracy and reduce complexity rather than a single CDF model. Because RMI trains only for each range of data, such as B-Tree, RMI can easily build with a simple model. In addition, this paper supports B-Tree. If learning data distribution does not fit for prediction, they use B-Tree

???????

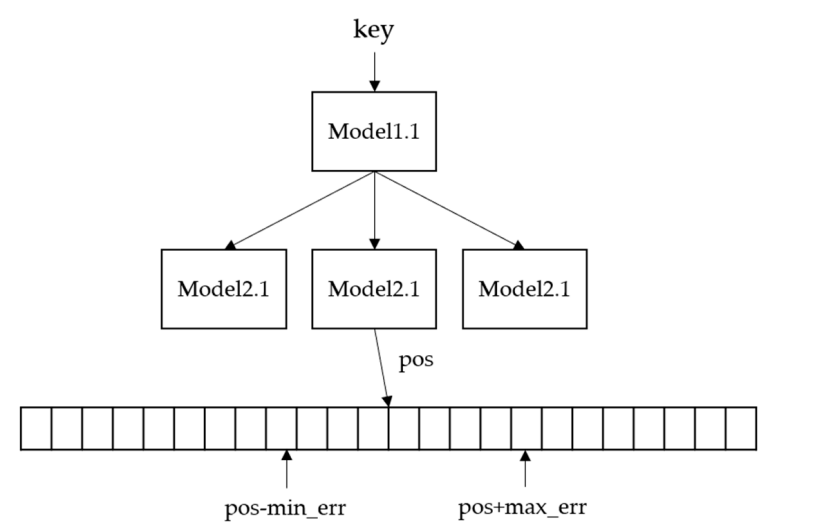Figure 4: Learned B-Tree

Conclusion

Reinforcement learning has proven to be a transformative approach in optimizing neural networks across a wide range of applications. By leveraging RL\'s dynamic learning capabilities, researchers have significantly advanced areas such as neural architecture search, hyperparameter tuning, model compression, and efficient deployment of neural networks. The adaptability of RL to learn from feedback and improve decision-making processes makes it uniquely suited to optimize complex, high-dimensional models. Despite its success, challenges remain. These include the high computational cost of RL algorithms, their reliance on extensive trial-and-error learning, and difficulties in ensuring stable and scalable performance in diverse real-world scenarios. Future research directions focus on improving sample efficiency, enhancing convergence stability, and integrating RL with complementary optimization paradigms like evolutionary algorithms and supervised learning. This evolving field highlights the potential for RL-driven solutions to push the boundaries of AI model performance and efficiency. However, addressing the associated challenges is crucial to making these techniques more accessible and practical for widespread use.

References

[1] Lee, D.; Noh, S.H.; Mim, S.L.; Cho, Y. LRFU: A block replacement policy which exploits systems and theory. IEEE Trans. Comput. 2001, 50, 1352–1361. [2] Nesbit, K.J.; Smith, J.E. Data cache prefetching using a global history buffer. In Proceedings of the Tenth Symposium on High-Performance Computer Architecture, Madrid, Spain, 14–18 February 2004. [3] Musser, D.R. Introspective Sorting and Selection Algorithms. Softw. Pract. Exp. 1997, 27, 983–993. [CrossRef] [4] Fu, J.W.; Patel, J.H.; Janssens, B.L. Stride directed prefetching in scalar processors. ACM SIGMICRO Newsl. 1992, 23, 102–110. [CrossRef] [5] Kim, J.; Pugsley, S.H.; Gratz, P.V.; Reddy, A.N.; Wilkerson, C.; Chishti, Z. Path confidence based lookahead prefetching. In Proceedings of the 2016 49th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), Taipei, Taiwan, 15–19 October 2016. [6] Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [CrossRef] [PubMed] [7] Kraska, T.; Beutel, A.; Chi, E.H.; Dean, J.; Polyzotis, N. The case for learned index structures. In Proceedings of the International Conferernce on Management of Data, Houston, TX, USA, 10–15 June 2018; pp. 489–504. [CrossRef] [8] Xiang, W.; Zhang, H.; Cui, R.; Chu, X.; Li, K.; Zhou, W. Pavo: A RNN-Based Learned Inverted Index, Supervised or Unsupervised? IEEE Access 2019, 7, 293–303. [CrossRef] [9] Jimnez, D.A.; Lin, C. Dynamic branch prediction with perceptrons. In Proceedings of the HPCA Seventh International Symposium on High-Performance Computer Architecture, Monterrey, Mexico, 19–24 January 2001; pp. 197–206. [10] Zhu, X.; Cheng, T.; Zhang, Q.; Liu, L.; He, J.; Yao, S.; Zhou, W. NN-sort: Neural Network based Data Distribution-aware Sorting. arXiv 2019, arXiv:1907.08817. [11] Sasaki, H.; Igarashi, H. Topology optimization accelerated by deep learning. IEEE Trans. Magn. 2019, 55, 1–5. [CrossRef] [12] Shamshirband, S.; Mosavi, A.; Rabczuk, T.; Nabipour, N.; Chau, K. Prediction of significant wave height; comparison between nested grid numerical model, and machine learning models of artificial neural networks, extreme learning and support vector machines. Eng. Appl. Comput. Fluid Mech. 2020, 14, 805–817. [CrossRef] [13] Gonçalves, R.; Ribeiro, V.M.; Pereira, F.L.; Rocha, A.P. Deep learning in exchange markets. Inf. Econ. Policy 2019, 47, 38–51. [CrossRef] [14] Mosavi, A.; Ardabili, S.; Várkonyi-Kóczy, A.R. List of Deep Learning Models. In Engineering for Sustainable Future; Springer: Berlin/Heidelberg, Germany, 2019; Volume 101, pp. 202–214. [CrossRef] [15] Kim, K.G. Deep learning book review. Nature 2019, 29, 1–73. [CrossRef] [16] Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [CrossRef] [17] Cecchetti, R.; de Paulis, F.; Olivieri, C.; Orlandi, A.; Buecker, M. Effective PCB Decoupling Optimization by Combining an Iterative Genetic Algorithm and Machine Learning. Electronics 2020, 9, 1243. [CrossRef] [18] Mijwil, M.M. Artificial Neural Networks Advantages and Disadvantages. Linkedin 2018, 1–2. Available online: https://www. linkedin.com/pulse/artificial-neural-networks-advantages-disadvantages-maad-m-mijwel/ (accessed on 2 April 2021). [19] Nabipour, N.; Dehghani, M.; Mosavi, A.; Shamshirband, S. Short-Term Hydrological Drought Forecasting Based on Different Nature-Inspired Optimization Algorithms Hybridized with Artificial Neural Networks. IEEE Access 2020, 8, 15210–15222. [CrossRef] [20] Jafarian, F.; Taghipour, M.; Amirabadi, H. Application of artificial neural network and optimization algorithms for optimizing surface roughness, tool life and cutting forces in turning operation. J. Mech. Sci. Technol. 2013, 27, 1469–1477. [CrossRef] [21] Askarzadeh, A.; Rezazadeh, A. Artificial neural network training using a new efficient optimization algorithm. Appl. Soft Comput. J. 2013, 13, 1206–1213. [CrossRef] [22] Zappone, A.; Di Renzo, M.; Debbah, M.; Lam, T.T.; Qian, X. Model-Aided Wireless Artificial Intelligence: Embedding Expert Knowledge in Deep Neural Networks for Wireless System Optimization. IEEE Veh. Technol. Mag. 2019, 14, 60–69. [CrossRef] [23] Jiang, J.; Fan, J.A. Simulator-based training of generative neural networks for the inverse design of metasurfaces. Nanophotonics 2019, 9, 1059–1069. [CrossRef] [24] Mutlag, A.H.; Shareef, H.; Mohamed, A.; Hannan, M.A.; Abd Ali, J. An improved fuzzy logic controller design for PV inverters utilizing differential search optimization. Int. J. Photoenergy 2014, 2014. [CrossRef] [25] Aljarah, I.; Al-Zoubi, A.M.; Faris, H.; Hassonah, M.A.; Mirjalili, S.; Saadeh, H. Simultaneous Feature Selection and Support Vector Machine Optimization Using the Grasshopper Optimization Algorithm. Cogn. Comput. 2018, 10, 478–495. [CrossRef]

Copyright

Copyright © 2024 Moussa Mohamed Naji Haqi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.